[Leetcode] 124. Binary Tree Maximum Path Sum
Identifying the Problem
이진트리를 순회하면서, 가장 큰 path sum을 구한다.
단, 노드는 최대 한번만 path에 나타나야한다.
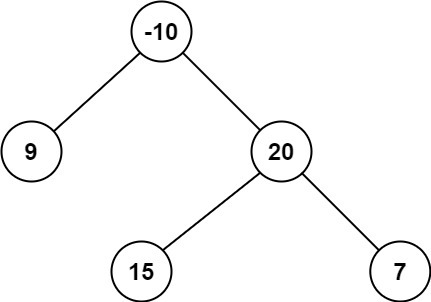
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Organizing thoughts
tree를 중위 순회하면서, 합을 누적시키다가, 합이 음수가 되면,
sum을 다시 0으로 초기화하고 최대값을 구해 나간다.
하지만 이렇게 쉽게 풀리면 hard가 아니라 easy이다.
작성한 코드를 제출했지만 내가 생각한 답과 달랐다.
Mistake
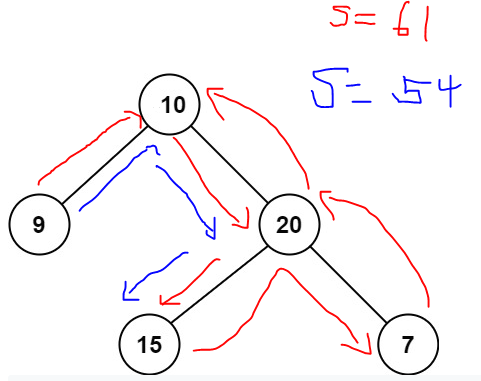
path의 개념을 잘못 이해했다.
하나의 선이 있다면 그 선이 노드에 한번만 걸쳐가게 해야하는데,
그 선이 노드를 두번 걸치게 되는 줄 알았다.
중위 탐색의 순서를 배열로 생각했을 때 가장 큰 max subarray를 구하는 문제로 착각했던 것이다.
Sourcecode
## 내가 짠 코드
class Solution {
int sum = 0;
public:
int maxPathSum(TreeNode* root)
{
if(!root) return 0;
maxPathSum(root->left);
sum+=root->val;
cout<< sum << '\n';
if(sum < 0) sum = 0;
maxPathSum(root->right);
return sum;
}
};## 정답 코드 및 출처
[recommend for beginners]clean C++ implementation with detailed explanation - LeetCode Discuss
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
이 곳에서 각 tree 별 case를 확인 할 수 있다.
[Leetcode][124] Binary Tree Maximum Path Sum
문제 : https://leetcode.com/problems/binary-tree-maximum-path-sum/ 서브트리의 루트 노드를 기준으로 만들 수 있는 sequence들은 다음과 같다. 1. 현재 루트노드, 루트노드의 왼쪽, 오른쪽 노드를 sequenc..
withhamit.tistory.com
class Solution {
int sum;
public:
int maxPathSum(TreeNode* root)
{
sum = INT_MIN; //적어도 최소 하나는 더해야 하기에
//0이 아닌, 가장 작은 int값을 최소값으로 설정
help(root);
return sum;
}
int help(TreeNode* root)
{
if(!root) return 0; //재귀 탈출
int left = max(0,help(root->left)); //case 2
int right = max(0,help(root->right)); //case 3
sum = max(sum , left + right + root->val);
//case 1 : root와 left,right가 기존 sum 보다 크다면 셋의 합을 sum으로 한다.
return max(left,right) + root->val;
//case 4 left, right가 음수면, left와 right를 정하는 과정에서 l,r을 버린다.
}
};'Algorithm' 카테고리의 다른 글
| [Leetcode] 98. Validate Binary Search Tree (0) | 2021.09.14 |
|---|---|
| [Leetcode] 102. Binary Tree Level Order Traversal (0) | 2021.09.11 |
| [Leetcode] 226. Invert Binary Tree (0) | 2021.09.09 |
| [Leetcode] 104. Maximum Depth of Binary Tree (0) | 2021.09.09 |
| [Leetcode] 647. Palindromic Substrings (0) | 2021.09.09 |








